Q1
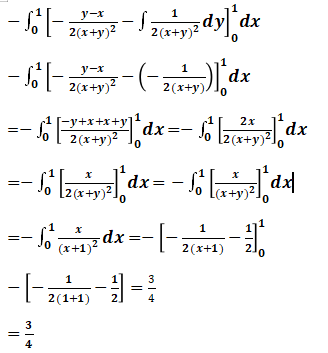
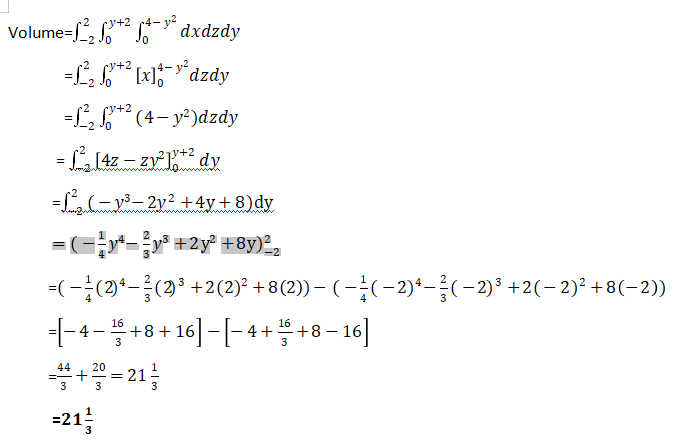
Hence becomes
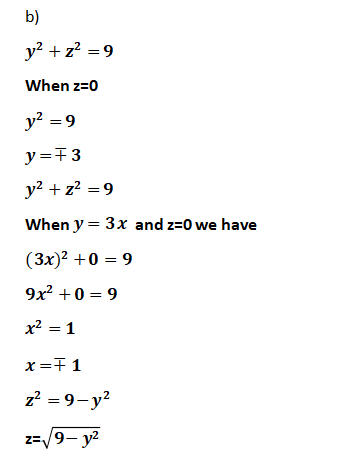
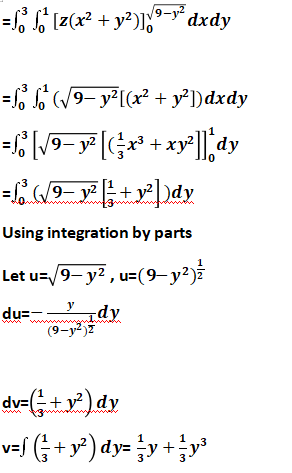
Applying integration by parts we obtain
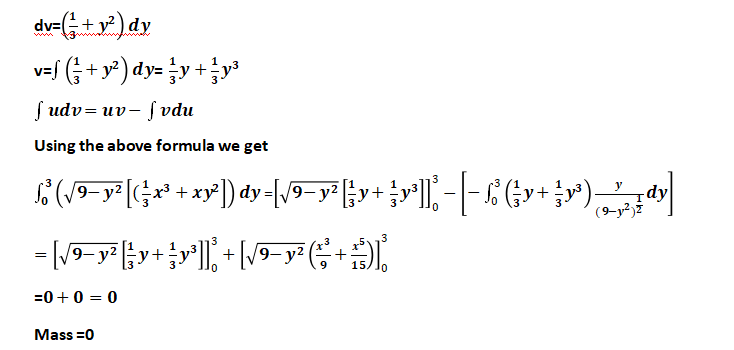
=
=
Hence becomes
Applying integration by parts we obtain
Q2)
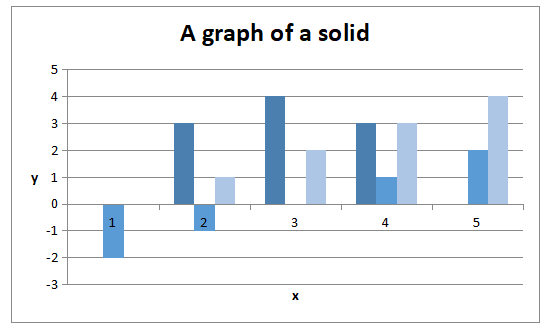
A solid is described by S=,-2.
| x | y | z |
| 0 | -2 | 0 |
| 3 | -1 | 1 |
| 4 | 0 | 2 |
| 3 | 1 | 3 |
| 0 | 2 | 4 |
Volume=
=
=
=
=
=
=
=
=
c) Volume=
=
=
=
=
=
=
=
=
=
=
Q3)
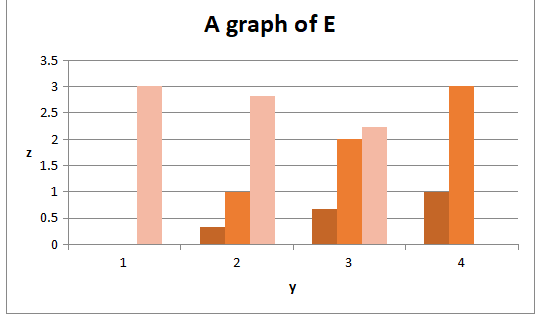
a)
When z=0
When and z=0 we have
| x | y | z |
| 0 | 0 | 3 |
| 1 | 2.828 | |
| 2 | 2.236 | |
| 1 | 3 | 0 |
b)
When z=0
When and z=0 we have
z=
=
=
=
=
=
Using integration by parts
Let u= , u=
du=
dv=
v==
Using the above formula we get
=
=
Mass =0