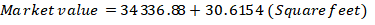Multiple regression model
In this section we present a multiple regression to estimate the market value as a function of both size and age of the house.
The hypothesis we sought to test is;
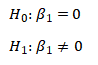
The results of the regression equation are given below;
Table 1 below presents the summary output where we can see the value of R-Squared (R2) to be 0.6501; this implies that 65.01% of the variation in the market value is explained by both the age and the size of the house.
| Table 1: SUMMARY OUTPUT | |
| Regression Statistics | |
| Multiple R | 0.806281 |
| R Square | 0.650088 |
| Adjusted R Square | 0.630649 |
| Standard Error | 5733.075 |
| Observations | 39 |
Table 2 below gives the ANOVA table where we can see that the overall model is significant at 5% level of significance (p < 0.05).
| Table 2: ANOVA | |||||
| df | SS | MS | F | Significance F | |
| Regression | 2 | 2.2E+09 | 1.1E+09 | 33.44156 | 6.18E-09 |
| Residual | 36 | 1.18E+09 | 32868148 | ||
| Total | 38 | 3.38E+09 |
Table 3: Regression coefficients
| Coefficients | Standard Error | t Stat | P-value | Lower 95% | Upper 95% | |
| Intercept | 34336.88 | 10862.85 | 3.160945 | 0.003184 | 12305.99 | 56367.76 |
| House Age | 125.6974 | 427.7699 | 0.293844 | 0.770565 | -741.86 | 993.255 |
| Square Feet | 30.61539 | 4.560027 | 6.713861 | 7.81E-08 | 21.36723 | 39.86356 |
From table 3 above, we can see that only the size of the house significantly predicts the market value of the house (p < 0.05), the age of the house does not significantly predict the market value of the house (p > 0.05).
The coefficient of the intercept is 34336.88; this implies that holding the age and the size of the house constant, we would expect the market value of the house to be 34336.88.
The coefficient of square feet (size of the house) is 30.6154; this implies that a unit increase in the size of the house is expected to result in an increase in the market value of the house by 30.6154. Similarly, a unit decrease in the size of the house is expected to result in a decrease in the market value of the house by 30.6154.
Considering only the significant variables, the estimated regression equation would be given as follows;