For each true-false statement: Replace the small response line with a T or F (capital, black, bold).
Part I True-False Statements: Fill in T or F (4 points each)
- In a regression involving age and serum cholesterol level, the “least squares” or “best fit” line calculated from the sample data estimates the age-adjusted mean serum cholesterol level in the population. _F__
XXX
- R2, the coefficient of determination, decreases when a variable is removed from a regression model. _T__
XXX
- The following data are from a follow-up study investigating a possible relationship between elevated ferritin levels (>200 µg/l) and ischemic stroke:
| Exposed | Unexposed | |
| Events | 56 | 37 |
| Person-time | 819 | 951 |
The appropriate procedure for evaluating the significance of such data is the binomial test. _F__
XXX
- The maximum likelihood method is used to estimate parameters in logistic regression? _T__
XXX
- In a logistic regression model with 2 predictor variables (risk factors A and B) and no interaction term, the estimated relative risk (RR) for subjects exposed to both risk factor A (adjusted RR estimate = 2.0) and risk factor B (adjusted RR estimate = 1.5) is 3.0. _F__
XXX
Part II Brief Responses (4 points each)
For questions 1 – 5: Replace the small response line with your letter choice (capital, black, bold) or fill-in response (black, bold).
- Part 1: For a fixed sample size: as the number of independent variables in a regression model increases, the power of the regression decreases.
XXX
- increases
- decreases
Part 2: When a potential confounding variable is found not to affect the β-coefficient estimate for the variable of interest in a regression model and is therefore removed from the model, the coefficient of determination (R2) decreases
XXX
a) increases
b) decreases
- An F-test for homogeneity of variances (i.e. Bartlett’s test) must be performed prior to conducting an analysis of covariance (ANCOVA).
XXX
- Part 1: Under what circumstances are chi-square tests biased? all of the above
XXX
- if any expected value is less than 1.0 or > 20% of the expected values are less than 5.0
- small sample size
- when there is 1 degree of freedom
- all of the above
Part 2: What is the best statistical test to apply when dealing with simple case-control data (single 2 x 2 table)? _Fisher exact test__
XXX
- chi-square test
- fisher exact test
- binomial test
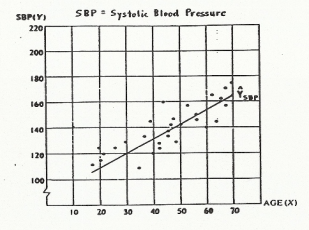
- Refer to the figure below:
Part 1: What is the estimated mean SBP for age 40? __130________
XXX
Part 2: What is the estimated mean SBP for age 10? __100________
XXX
- As health commissioner of city B you have decided to implement a $10 million exercise program if results from a recently concluded cohort study in 2,000 males aged 40-59 years showed there was 95% confidence (exact binomial) that the relative risk (RR) among subjects with a baseline resting heart rate (HR) > 80 beats/min vs. those with a baseline resting HR ≤ 80 beats/min was different from 1.50. The estimated RR from the study was 2.61 (X2 = 13.431).
After calculating a test-based 95% confidence interval for the estimated RR in the space below: What is your decision? __Implement the program_
XXX
- Implement the program.
- Do not implement the program.
For questions 6 – 7: Replace the response line with your brief statement (black, bold).
- Part 1: Name one limitation when using the Mantel-Haenszel method to control for confounding in case-control studies.
XXX
The method is intricate and demands a relatively large sample size in situations where there is more than one confounder because of the high number of strata
Part 2: Name one limitation when using matching to control for confounding in a case-control study?
XXX
The method can lead to over-adjustment and even introduce confounding. Also, matching can create selection bias when used for non-confounders.
- Name 2 types of censoring that can occur during follow-up in a cohort study or clinical trial.
XXX
1. Right censoring
2. Left censoring
For question 8: Replace the small response line with your letter choice (capital, black, bold).
- A potential confounding variable should be included in a multiple proportional hazards regression model if
Choice A and B
XXX
- it is an independent risk factor for the outcome
- it is a statistically significant predictor for the outcome
- it differs in frequency between exposed and unexposed study subjects
- choices a and b
- choices a and c
- all of the above
- Using a diagram, show how the total sum of squares is partitioned in a 2-factor mixed ANOVA?
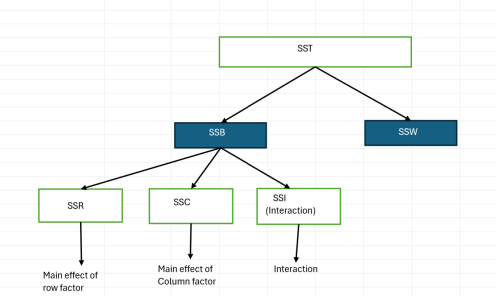
For question 10: Replace the small response line with your fill-in response (black, bold).
- Part 1: Mantel-Haenszel method is used to analyze matched-pair case-control studies with multiple confounding variables.
XXX
Part 2: Multiple regression analysis is used to analyze cohort studies with multiple confounding variables.
XXX
Part III. Problems (10 points each)
1. A study was performed to evaluate a potential relationship between diastolic blood pressure (DBP) and exercise minutes per week in a random sample of 11 subjects aged 20 to 29 years.
The results were as follows:
Exercise (min/week) DBP (mm Hg)
10 80
20 73
30 81
40 83
50 77
60 75
70 78
80 77
90 76
100 72
110 73
Using the attached SAS file (SASfinal1.sas), perform a simple linear regression analysis with the dependent variable, DBP, and independent predictor variable, Exmin/week.
Assume normality and equal variance. Use α = 0.05 (two-tailed) and assume 60% power.
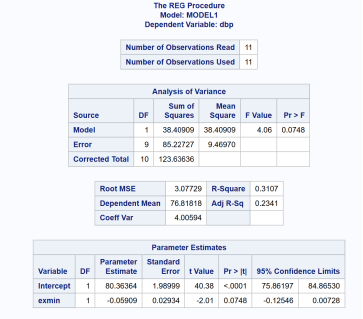
- State the null and alternative hypotheses for testing the slope.
XXX
Null hypothesis Ho: β1 = 0
Alternative hypothesis Ha: β1 ≠ 0
- List the critical value for testing the slope.
XXX
tc =2.262
- List the R2.
XXX
R2 = 0.3107
- Replacing the response lines, report your decision (reject Ho and accept Ha OR fail to reject Ho) based on the critical value, P-value, and 95% confidence interval for the slope:
Since t-statistic < critical value, fail to reject Ho
_________________________________________________________________________
XXX
Since P-value > 0.05, fail to reject Ho____________________________
XXX
Since 95% CI includes the null value, fail to reject Ho
__________________________________________________________________________
XXX
- If the decision was to fail to reject Ho, can Ho be accepted?
XXX
No, the Ho cannot be accepted. Failing to reject the null is not an indication that it is true. It only means that the test does not provide enough evidence to reject the null.
2. In an epidemiologic study, 147 incident breast cancer cases were compared to 179 controls selected from the population that gave rise to the cases with respect to alcohol consumption history. The data were as follows:
| Exposure status | Disease Status | ||
| Case | Control | Total | |
| > 3 drinks/day | 75 | 87 | 162 |
| Nondrinker | 72 | 92 | 164 |
| Total | 147 | 179 | 326 |
Perform the appropriate statistical test of the relationship between breast cancer and alcohol consumption history using the attached SAS file (SASfinal2.sas). Assume α = 0.05 (two-tailed) and 80% power.
- State the null and alternative hypotheses.
XXX
Null hypothesis Ho: Disease status is independent of exposure status
Alternative hypothesis Ho: Disease status is dependent on exposure status
- List the critical value.
XXX
= 3.841
- List the estimated odds ratio.
XXX
OR = 1.1015, 95% CI {0.7120, 1.7043}
- Replacing the response lines and using the uncorrected chi-square, P-value, and odds ratio output from SAS, report your decision (reject Ho and accept HA OR fail to reject Ho) based on the critical value, P-value, and 95% confidence interval for the odds ratio.
Since chi-square statistic < critical value, fail to reject Ho
__________________________________________________________________________
XXX
Since P-value > 0.05, fail to reject Ho
_______________________________________________________________________
XXX
Since 95% CI includes the null value, fail to reject Ho
_________________________________________________________________________
XXX
- If the decision was to fail to reject Ho, can Ho be accepted?
XXX
No, the Ho cannot be accepted. Failing to reject the null is not an indication that it is true. It only means that the test does not provide enough evidence to reject the null.
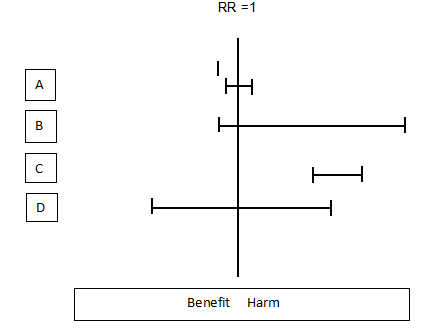
- Epidemiologic study results, expressed as point estimates with accompanying 95% confidence intervals, are shown in the diagram below. For A–D, list the number of each description that applies to the confidence interval as follows:
A: 1, 2, 3, 4, …
B: 1, 2, 3, 4, … and so on.
Among A-D there are 10 total correct descriptions.
Each correct description earns 1 point.
Each incorrect description subtracts 1 point.
- Reject Ho
- Do not reject Ho
- Imprecision
- Accept Ho
- Likely type II error
- Cannot distinguish between benefit and harm
- Clear elevation of risk
A: 2, 6
B: 2, 6, 7
C:1, 7
D: 2, 6,
RR =1
In Module 5 (Slide 12) we used a two-sample t-test to compare the mean resting heart rate for normal males aged 40-59 in city A to the mean resting heart rate for normal males aged 40-59 in city B. (10 points)
The data were as follows:
| City A | City B | ||
| Age (yr) | HR (beats/min) | Age (yr) | HR (beats/min) |
| 52 | 71 | 67 | 74 |
| 67 | 83 | 61 | 69 |
| 58 | 74 | 60 | 69 |
| 51 | 66 | 62 | 71 |
| 59 | 75 | 59 | 70 |
| 53 | 70 | 63 | 73 |
| 58 | 76 | 61 | 72 |
| 61 | 78 | 56 | 59 |
| 49 | 69 | 69 | 76 |
| 64 | 80 | 60 | 68 |
Note: Age of the study subjects was not included in the original dataset.
Assume normality and equal variance. Use α = 0.05 (two-tailed).
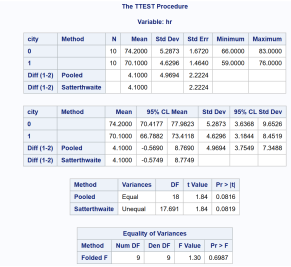
Using the attached SAS file (SASfinal4.sas):
- State the null and alternative hypotheses for an unadjusted two-sample t-test comparing HR between city A and city B.
XXX
Null hypothesis Ho: The mean resting heart rate for males aged 40-59 is equal in City A and City B. i.e., µA = µB
Alternative hypothesis Ha: The mean resting heart rate for males aged 40-59 is not equal in City A and City B. i.e., µA ≠ µB
- List the critical value.
XXX
tc =2.101
- Replacing the response line, report your decision (reject Ho and accept Ha OR fail to reject Ho) based on the critical value.
XXX
_Since t-statistic < critical value, fail to reject Ho
To adjust for potential confounding due to age, a 1-way ANCOVA model was fit to the data.
In the test for interaction between the covariate (age) and treatment (city A vs. city B):
Full Model: Y = β1X1 + β2X2 + β3X1X2 + ε
Reduced Model: Y = β1X1 + β2X2 + ε
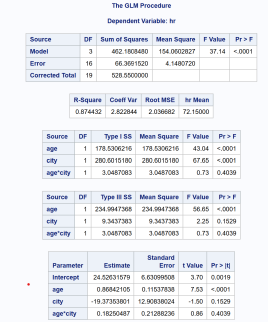
- State the null and alternative hypotheses for the test for interaction.
XXX
Null hypothesis Ho: There is no interaction between age and city. i.e., β3 = 0
Alternative hypothesis Ha: There is an interaction between age and city. i.e., β3 ≠ 0
- From the SAS output, what is the estimate for the interaction term (age*city)?
XXX
β3 = 0.1825
- Is the interaction term statistically significant?
XXX
No, the interaction is not statistically significant because p >0.05.
- Can the ANCOVA process proceed?
XXX
Yes, the ANCOVA Process can proceed for the main effects because the interaction is not statistically significant.
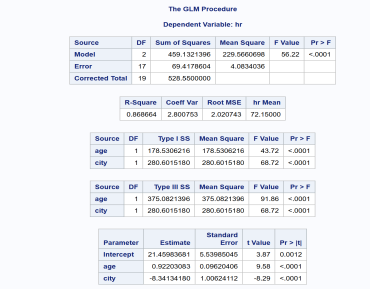
In the test for the age-adjusted treatment effect:
Full Model: Y = β1X1 + β2X2 + ε
Reduced Model: Y = β1X1 + ε
- State the null and alternative hypotheses for the test of adjusted treatment difference.
XXX
Null hypothesis Ho: There is no difference in adjusted mean heart rates between City A and City B. i.e., β2 = 0
Alternative hypothesis Ha: There is a significant difference in age-adjusted mean heart rates between City A and City B. i.e., β2 ≠ 0
- From the SAS output, what is the estimate for the adjusted treatment effect (city)?
XXX
β2 = -8.3413
- Is the age-adjusted treatment effect statistically significant?
Yes, the age-adjusted treatment effect is statistically significant because p<0.05
XXX
