Introduction
The project is focussed on dynamical billiard theory. The dynamic system is based on collision model. The model which are made for this system are conic section of: ellipse, polar n-petal, parabola n-petal and Hyperbola.
Set up
Conic section boundaries:
Ellipse
Ellipse equation is defined as
A point c on the minor axis is defined as
Where a and b are major and minor axis of the ellipse
For finding the foci of the ellipse, let and
Then
The boundary point of ellipse are calculated using sage (Popel, 2014).
Therefore the foci of the ellipse is given as (0,12) (0,-12)
Hence for centre (0,0)
The equation of the ellipse is
Conic section of Ellipse
For different centres of the ellipse, centre (h,k)
The equation becomes,
Here x is replaced as x – h and y is replaced as y – k
Let and
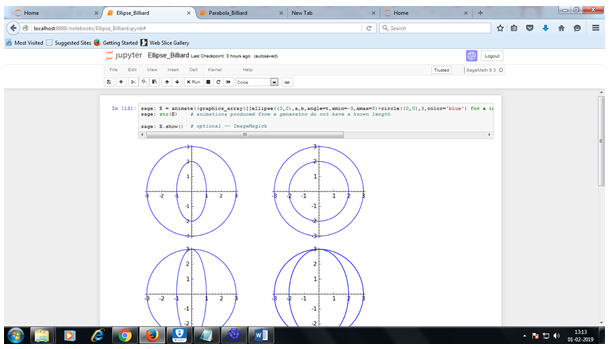
Polar n-petal
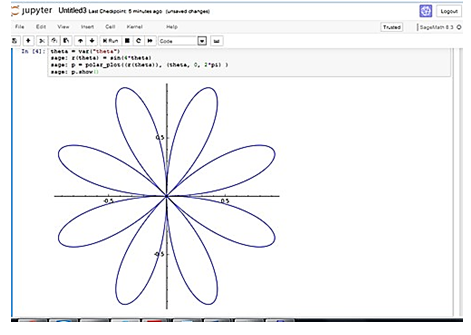
Conic section of Polar n-petal
To calculate the cross section of the petal, let us consider the polar coordinate system that defines the angle and distance (Timur, Adzkiya and Soleha, 2018).
Polar coordinate specified at a point is given as
where is the distance and is the angle
Area of one petal = times integral of
The petal is integrated with respect to with a specific interval.
value is taken as
Thus the area of one petal gives the cross section of one petal.
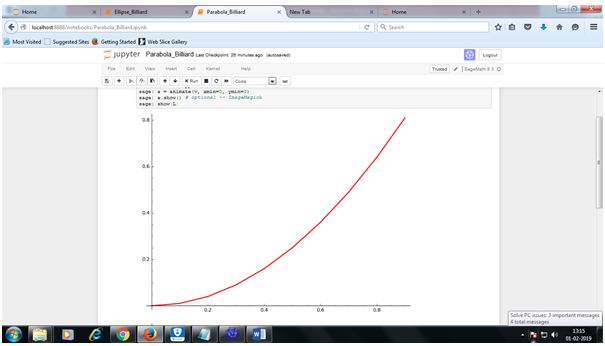
Parabola
Conic section of Parabola n-petal
To determine the conic section of parabola, let us calculate the focus and the directrix of the parabola.
We know that the equation of the parabola is given as,
Let us consider where c is the focus of the parabola.
Thus,
Say for c=2, the focus is 2 from the vertex and directrix also have the same value of 2 from the vertex.
We can compare the vertex with same value and with different value of the parabola.
| Vertex at | Vertex at |
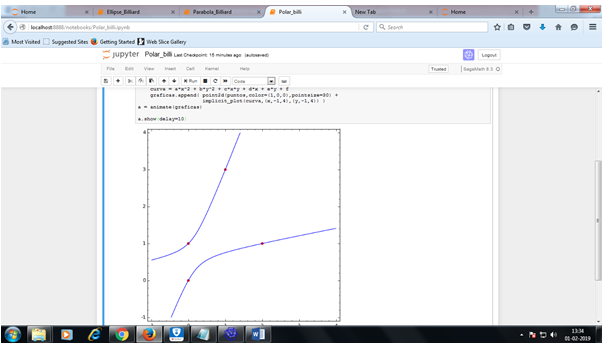
Hyperbola
Determine the walls
Elliptic curve
Calculation for the new_position routine of the families
Ellipse
The equation of the ellipse is given by
The major axis and minor axis of the ellipse is obtained from the diameter of the ellipse.
The longest diameter is major axis and shortest diameter is minor axis.
Let us consider a as major axis and b as minor axis and the distance from the centre of one of the foci is c.
The circumference of the major axis is 2a, which when extended form a triangle.
By using Pythagoras theorem,
or ———(1)
To determine x and y points on an ellipse, let and be the distance from the x,y coordinate placing the ellipse at the centre of the ellipse, the points will be and
Now the length of the distance from the x,y coordinate =
We know that the distance at any point on the x,y coordinate is given as
Now substituting the points and in the above equation
We have
On simplifying and factorising and divide throughout by ,
Eliminating the common terms we have
Using (1), we have
Parabola
The equation of the parabola is given by
To determine the focus and the directrix of the parabola, consider a point c from the vertex on the parabola, say
When determining the axis, we have to calculate the vertical and horizontal axis of parabola
Since axis of symmetry is , we are considering the vertical and horizontal axis of parabola.
The standard equation of a parabola with vertical axis is given by
——-(2)
Equation (1) after multiplying both the sides by 2, can be rewritten as,
—–(3)
For simplicity of the problem, let h=0 and k=0, then equation (2) becomes,
On comparing equation (2) and (3), we have
Substituting the value of p in equation (4), we have
The above equation simply resembles the equation of the parabola.
On comparing the vertex and focus of the parabola, we have
| Vertex | Focus |
| (0,0) | (0,1/2) |
| (h,k) | (h,k+p) |
And the directrix is given as
Thus any point on the parabola, is the distance to the focus is the same distance to the directrix.
Calculation for the new_velocity routine of the families
Parabola
Projectile motion is described as the objects that are dropped, thrown straight up, or thrown straight down. The height of the objects depends on the parameters such as the height from which the objects are dropped or thrown, upward/downward velocity. and the pull of gravity downward on the object. The acceleration due to gravity is approximately 32 feet/second2 (or 9.8 meters/second2).
The general formula is given by
The above formula is a quadratic equation and it’s graph is a parabola.
is initial velocity
Consider two cases:
Objects that are dropped:
There is no initial velocity other than the pull of gravity, if the object is just dropped and not thrown. That is v0= 0. The term “h” represent the height and h0 to represent the initial height.
The object is modelled for t seconds after it has been dropped is given by the formula:
Objects that are thrown:
A certain amount of initial velocity is required when the object is thrown from somewhere. In this case, there is some initial velocity. The term “h” is used to represent the height and h0 is used to represent the initial height.
The object is modelled with the height for t seconds after it has been thrown is given by the formula:
Periodic points and Stability calculations
Elliptical orbits are more stable than circle. Circular orbits are a special sub-set of ellipses. The points in the ellipse are stabilised by increasing the aspect ratio of the ellipse. Thus the points in the ellipse are made stable. If the points are made stable, it gets changed into any polygon shape.
Simulation
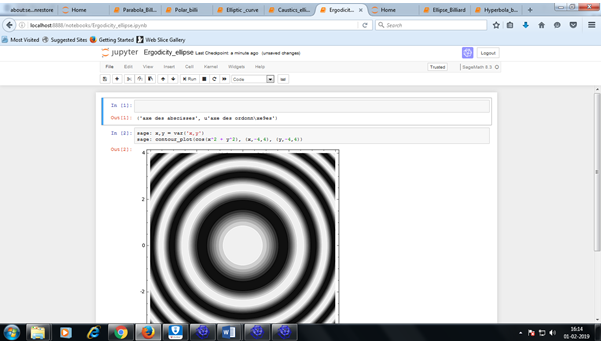
Caustics for the no-slip ellipse
Ergodicity of stable elliptic points
References
Cui, J., Lei, X., Tu, X. and Wang, H. (2013). Reacher on Ellipticity Error by Use of Minimum Circumscribed Ellipse and Maximum Inscribed Ellipse Algorithm. Applied Mechanics and Materials, 333-335, pp.1461-1464.
Péterfalvi, C., Pályi, A., Rusznyák, Á., Koltai, J. and Cserti, J. (2010). Catastrophe optics of caustics in single and bilayer graphene: Fine structure of caustics. physica status solidi (b), 247(11-12), pp.2949-2952.
Popel, M. (2014). THE METHODICAL ASPECTS OF THE ALGEBRA AND THE MATHEMATICAL ANALYSIS STUDY USING THE SAGEMATH CLOUD. Information Technologies in Education, (19), pp.93-100.
Snieder, R. and Sens-Schönfelder, C. (2015). Seismic interferometry and stationary phase at caustics. Journal of Geophysical Research: Solid Earth, 120(6), pp.4333-4343.
Timur, T., Adzkiya, D. and Soleha (2018). Simulations of linear and Hamming codes using SageMath. Journal of Physics: Conference Series, 974, p.012064.
Tsukada, T. (2013). Genericity of Caustics on a corner. Journal of Singularities.
Vogelsberger, M. and White, S. (2011). Streams and caustics: the fine-grained structure of Λ cold dark matter haloes. Monthly Notices of the Royal Astronomical Society, 413(2), pp.1419-1438.
Zirakashvili, N. (2017). Study of deflected mode of ellipse and ellipse weakened with crack. ZAMM – Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik, 97(8), pp.932-945.