Introduction, Background and Project Overview
A dynamic problem can be split in two steps: obtaining the equation of motion and solving it. To obtain the equation of motion we use common dynamics theory, such as Newton’s second law. The equation of motion can then be solved through analytical or numerical techniques. So far, you have mostly looked at analytical solutions to problems, however, even for simple dynamics problems these can rapidly become complex and unwieldy. In actuality, the presence of a true analytical solution is rare in many real-world problems and rely on simplifications and assumptions (e.g. neglecting drag). Numerical solutions on the other hand can be readily used to solve simple and complex dynamics problems. For numerical solutions the main challenges become computational resources and the elegance of the model.
Elastic pendulum (also called spring pendulum or swinging spring) is a physical system where a piece of mass is connected by a spring. Compared with the ideal pendulum, not only angle, but also the length of string (spring) is changing in the process, which makes the problem nonlinear, and extremely difficult to solve analytically. An example in reality for elastic pendulum is the bungee jump. In this assignment, we will first try to get the analytical solution for elastic pendulum with multiple approximations. Then finite difference method will be adopted to get the numerical solution. In the end, we will try to build up a simple numerical model for the whole bungee jump process.
| Figure 1. The schematic graph for an elastic pendulum. The grey curve is the trajectory of the mass. | Table 1. Physical quantities in the system.PropertySymbolQuantityUnitItem Total mass 0.1kgInitial angle 0.05 Initial angular velocity 0.01rad/sInitial radius velocity 0.1m/sSpring Free length 20mInitial elongation 2mElastic coefficientk20N/m |
For the following questions:
- This elastic pendulum is swinging in one plane, so two dimensional coordinate system is adequate to describe the system.
- The equation of motion for a harmonic oscillator is in the form of :
and are constants, which can vary in different equation of motion, and need to be found by rearranging. Such form of equation has the analytical solution like:
Where
| Angular frequency | |
| Amplitude | |
| Phase |
- Small angle theorem: when , cos.
Equation of Motion
- Draw the free body diagram for the elastic pendulum model in the Fig 1. Write down the equations of motion in polar coordinate systems, and Cartesian coordinate system.
| Answer within this box. Change the size of the box if needed. |
| Figure 2: The free body diagramPolar coordinates () (t) + a. =0 In Cartesian coordinates, the equation becomes Tan = = Therefore in Cartesian coordinates the equation becomes + a.( –c) = 0 |
Analytical Solution
- To get the analytical solution, for a tough spring and a small mass, we can use the following assumption:
- The elastic pendulum does harmonic oscillation in θ and r direction.
- In r direction, the oscillation of the spring is the dominate motion, and terms relevant with θ can be ignored.
- In θ direction, the change of the spring length can be ignored, terms with r can be ignored.
Arrange the equation of motion in polar coordinate system to the harmonic oscillation form: (1) use small angle theorem first, (2) then delete extra non-linear terms for approximation. Get the analytical solution of elastic pendulum with the parameters in the table 1.
| Answer within this box. Change the size of the box if needed. |
| , () (t) + a. =0 … Since it is known that , and , the exact solution now becomes; and Given that and = 0.1 rad/s = |
Finite Differences
- Write down the equation of motion in Cartesian coordinate system from Question 1 in the finite difference form. State the initial conditions for finite difference method. Show all working.
| Answer within this box. Change the size of the box if needed. |
| Expressing the equation in terms of x and y = x( = y(The equation of motion can be rewritten as follows; + a.( –c) = 0 |
MATLAB Code
- Show the MATLAB code for solving the finite difference equations obtained in Question 3.
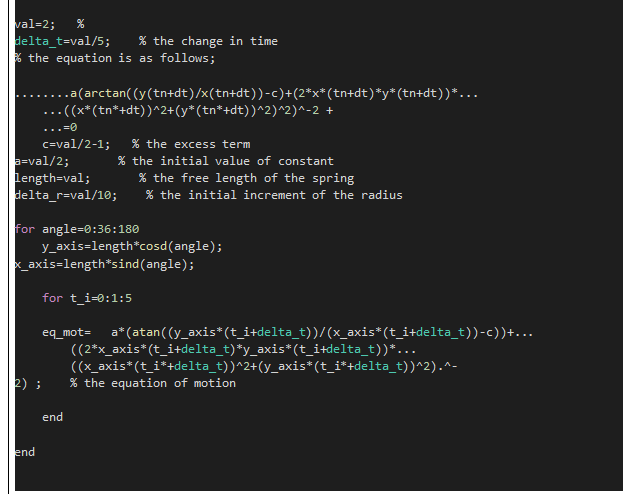
| Answer within this box. Change the size of the box if needed.(Include initialisation based on Question 3. Do not include the code part responsible for the plotting.) |
| val=2; %delta_t=val/5; % the change in time % the equation is as follows; ……..a(arctan((y(tn+dt)/x(tn+dt))-c)+(2*x*(tn+dt)*y*(tn+dt))*… …((x*(tn*+dt))^2+(y*(tn*+dt))^2)^2)^-2 + …=0 c=val/2-1; % the excess term a=val/2; % the initial value of constant length=val; % the free length of the spring delta_r=val/10; % the initial increment of the radius for angle=0:36:180 y_axis=length*cosd(angle); x_axis=length*sind(angle); for t_i=0:1:5 eq_mot= a*(atan((y_axis*(t_i+delta_t))/(x_axis*(t_i+delta_t))-c))+… ((2*x_axis*(t_i+delta_t)*y_axis*(t_i+delta_t))*… ((x_axis*(t_i*+delta_t))^2+(y_axis*(t_i*+delta_t))^2).^-2) ; % the equation of motion end end |
Discretization and Convergence:
- The accuracy of numerical solution is completely dependent on the timestep . The accuracy and the computational cost both increase indefinitely as . Because of this, in practical application of computational resources, we are only interested in which will provide results that do not change/benefit from any further increase in resolution.
1) Estimate the dt value according to the frequency in Question 2. There should be at least 40 points in one period in each direction.
2) Plot the trajectory of the elastic pendulum from the numerical solution (x-y plot), with at least 2 periods in each direction.
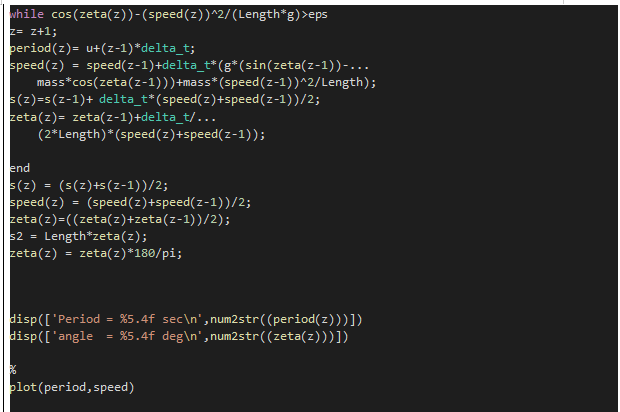
| Answer within this box. Change the size of the box if needed. |
| FDMz=1;% THE TERMS FROM THE TABLE AS FOLOWS Length=2; % Spring length mass=0.4; % bob mass delta_t = 0.001; % small change in timeg=9.981; % force of gravity % empty vectorszeta= []; % the angle made when swinging speed = []; % the velocity period= []; % the time vector % Initializing Vectorsspeed(z)=5;zeta(z)=0;period(z)=0;s(z)=0;u=period(1); while cos(zeta(z))-(speed(z))^2/(Length*g)>epsz= z+1;period(z)= u+(z-1)*delta_t;speed(z) = speed(z-1)+delta_t*(g*(sin(zeta(z-1))-… mass*cos(zeta(z-1)))+mass*(speed(z-1))^2/Length);s(z)=s(z-1)+ delta_t*(speed(z)+speed(z-1))/2;zeta(z)= zeta(z-1)+delta_t/… (2*Length)*(speed(z)+speed(z-1)); ends(z) = (s(z)+s(z-1))/2;speed(z) = (speed(z)+speed(z-1))/2;zeta(z)=((zeta(z)+zeta(z-1))/2);s2 = Length*zeta(z);zeta(z) = zeta(z)*180/pi; disp([‘Period = %5.4f sec\n’,num2str((period(z)))])disp([‘angle = %5.4f deg\n’,num2str((zeta(z)))]) %plot(period,speed) |
Numerical solution VS Analytical solution:
- 1) Plot the x history (x-t plot) from numerical solution and analytical solution against each other on the same figure. Are they similar with each other? How about y history (y-t plot)?
2) Increase the mass and decrease the elastic coefficient in Table 1 as you like. Plot the trajectory from the numerical and analytical solution (x-y plot) with at least two periods in each direction. Which solution is more authentic and close to reality? Why?
| Answer within this box. Change the size of the box if needed. |
| val=2; %delta_t=val/5; % the change in time % the equation is as follows; ……..a(arctan((y(tn+dt)/x(tn+dt))-c)+(2*x*(tn+dt)*y*(tn+dt))*… …((x*(tn*+dt))^2+(y*(tn*+dt))^2)^2)^-2 + …=0 c=val/2-1; % the excess term a=val/2; % the initial value of constant length=val; % the free length of the spring delta_r=val/10; % the initial increment of the radius z=1;% THE TERMS FROM THE TABLE AS FOLOWS Length=2; % Spring length mass=0.4; % bob mass delta_t = 0.001; % small change in timeg=9.981; % force of gravity % empty vectorszeta= []; % the angle made when swinging speed = []; % the velocity period= []; % the time vector % Initializing Vectorsspeed(z)=5;zeta(z)=0;period(z)=0;s(z)=0;u=period(1); for angle=0:36:180 y_axis=length*cosd(angle); x_axis=length*sind(angle); for t_i=0:1:5 eq_mot= a*(atan((y_axis*(t_i+delta_t))/(x_axis*(t_i+delta_t))-c))+… ((2*x_axis*(t_i+delta_t)*y_axis*(t_i+delta_t))*… ((x_axis*(t_i*+delta_t))^2+(y_axis*(t_i*+delta_t))^2).^-2) ; % the equation of motion end end while cos(zeta(z))-(speed(z))^2/(Length*g)>epsz= z+1;period(z)= u+(z-1)*delta_t;speed(z) = speed(z-1)+delta_t*(g*(sin(zeta(z-1))-… mass*cos(zeta(z-1)))+mass*(speed(z-1))^2/Length);s(z)=s(z-1)+ delta_t*(speed(z)+speed(z-1))/2;zeta(z)= zeta(z-1)+delta_t/… (2*Length)*(speed(z)+speed(z-1)); ends(z) = (s(z)+s(z-1))/2;speed(z) = (speed(z)+speed(z-1))/2;zeta(z)=((zeta(z)+zeta(z-1))/2);s2 = Length*zeta(z);zeta(z) = zeta(z)*180/pi; disp([‘Period = %5.4f sec\n’,num2str((period(z)))])disp([‘angle = %5.4f deg\n’,num2str((zeta(z)))]) %plot(period,speed) |
Numerical Solution Application:
- Based on the finite difference code in Question 4, develop a new code for bungee jump simulation. Use the following set ups to adapt the code into the bungee system:
- When the distance between the person and the fixed end is less than the free length of the cord, the person does free fall/ projectile motion.
- When the distance between the person and the fixed end is more than the free length of the cord, the bungee cord applies the tension force and a damping force:
- To avoid entanglement of the cord, the distance between the two ends of the cord is at the beginning.
- The mass of the cord can be ignored. The mass of the person M = 60 kg.
The elastic coefficient k = 20 N/m. The free length of the cord is L0 = 20 m.
The initial velocity of the person is 0.
- Plot the trajectory of the person in the Cartesian coordinate in the first 60 seconds.
- Find the minimum distance to the ground and the cliff for the person to bungee jump safely.
- Show the velocity magnitude and acceleration magnitude history of the person in the first 60 seconds.
Hint: use if command in Matlab to switch between two equations of motions.
| Answer within this box. Change the size of the box if needed. |
| %Goal: Model the Spring Pendulum in 3-D with RK4 format ‘long’ mass = 0.1; %Mass in kg gravity = 9.81; %Gravity in m/s^2 k = 20; %Spring constant in N/m Length = 2; %Unstretched length of spring in m w = sqrt(k/mass); %Angular frequency of ossilations in rad/s x_0 = 3; %Initial x-position in m y_0 = 1; %Initial y-position in m z_0 = -2.2; %Initial z-position in m vx_0 = .1; %Initial x-velocity in m/s vy_0 = .2; %Initial x-velocity in m/s vz_0 = .3; %Initial x-velocity in m/s delta_t = .001; %Time step in s time = 20; %Total time to run simulation in s %Vectors store positions and velocities x_p = []; %Stores x-position y_p = []; %Stores y-position z_p = []; %Stores z-position x_velocity = []; %Stores x-velocity y_velocity = []; %Stores y-velocity z_veocity = []; %Stores z-velocity r_position = []; %Stores radial position velocity = []; %Stores total velocity for i = 1:time/delta_t r = sqrt(x_0^2 + y_0^2 + z_0^2); %Radial position %velocity in x direction dvx1 = delta_t*(-w^2*(1-Length/r)*x_0); dv_x2 = dvx1; dv_x3 = dv_x2; dv_x4 = dv_x3; v_xdirection = vx_0 + (dvx1 + 2*dv_x2 + 2*dv_x3 + dv_x4)/6; %Solves the y-velocity dvy1 = delta_t*(-w^2*(1-Length/r)*y_0); dvy2 = dvy1; dv_y3 = dvy1; dv_y4 = dvy1; vy = vy_0 + (dvy1 + 2*dvy2 + 2*dv_y3 + dv_y4)/6; %Solves the z-velocity dvz1 = delta_t*(-w^2*(1-Length/r)*z_0 – gravity); dvz2 = dvz1; dvz3 = dvz1; dvz4 = dvz1; v_zdirection = vz_0 + (dvz1 + 2*dvz2 + 2*dvz3 + dvz4)/6; %Solve the x-position d_x1 = delta_t*vx_0; dx2 = d_x1; dx3 = d_x1; dx4 = d_x1; x_position = x_0 + (d_x1 + 2*dx2 + 2*dx3 + dx4)/6; %Solve the y-position d_y1 = delta_t*vy_0; d_y2 = d_y1; d_y3 = d_y1; d_y4 = d_y1; y_position = y_0 + (d_y1 + 2*d_y2 + 2*d_y3 + d_y4)/6; %Solve the z-position d_z1 = delta_t*vz_0; dz2 = d_z1;dz3 = d_z1;dz4 = d_z1; z_position = z_0 + (d_z1 + 2*dz2 + 2*dz3 + dz4)/6; %Appends vectors to save all positions and velocities x_p = [x_p,x_0]; y_p = [y_p,y_0]; z_p = [z_p,z_0];x_velocity = [x_velocity,vx_0]; y_velocity = [y_velocity,vy_0];z_veocity = [z_veocity,vz_0]; r_position = [r_position,r];velocity = [velocity,sqrt(vx_0^2 + vy_0^2 + vz_0^2)]; %Set the current positions and velocities as the original to iterate. x_0 = x_position;y_0 = y_position; z_0 = z_position;vx_0 = v_xdirection; vy_0 = vy;vz_0 = v_zdirection; end %period vs position plot(1:time/delta_t,r_position) title(‘radial position against time’) |
Simple harmonic motion from a mass and spring system and that from a pendulum helps demonstrate about natural frequency. Vibration is an important part of understanding the nature of materials and their frequency.
The following equipment will contribute to the success of the lab exercise
- Data studio and a computer
- Table clamp
- Pendulum bob
- Mass hunger
- Stop switch
- Right angled rod clamp
- Spring
- meter stick
- balance scale
- support rod
- short rode
- Set of mass
- String
- Stop watch
- Motion sensor
- Force sensor
Procedure
Procedure
Simple pendulum
Mass of the bob was weighed and recorded. The bob was suspended from the bench by 1m string
Time t taken for bob to make a number of complete oscillations
Steps 1 and 2 were repeated using 0.8m , 0.6m, 0.4m and 0.2m.
Spring and mass
A small mass was hang from the spring. The masses were added progressively. In a table the masses were recorded with the corresponding increase in height.A new mass was added and the spring allowed to settle. The new height is recorded along with the weight.
The nest stage, data was collected using computer. Sensors were used to determine the height of the spring.
Complex harmonic motion is studied which is characterized by
- The system obeys hook`s law. This is to mean that displacement of the mass is directly proportional to displacement
Mv1=(m1+m2)v2
- The position of the mass when oscillating is sinusoidal in nature. That is to mean that if the graph of time against position is plotted, it will be a sine curve.
- The last trait of the system is that energy is conserved. The energy is not wasted through friction or air resistance.
There are some systems that do not meet one or more of these requirements and therefore are not classified as simple harmonic motion.
Natural frequency is oscillating system is given by
=
Period of the system is given by
T = 2
Pendulum on the other hand has a restoring force that do not obey hook`s law, the gravity
F =-mg sin ϴ
When dealing with a small angle
F =-mg ϴ = -mg(x/l)
Mg/l is the effective k
T = 2
Background
The
Procedure
Elastic pend
ulum
Mass of the bob was weighed and recorded. The mass of the steel ball was measured and recorded. The ball was placed on the pendulum catcher and the distance between pivot and the balance pivot of the pendulum and the ball.The pendulum was reconnected
The ball was shot such that it was trapped by the pendulum and the maximum angle ϴ3 recorded.
The set up is as shown in the figure below;
Figure 1: The elastic pendulum set up
The table below indicates the values of each of the components of the set up.
| Property | Symbol | Quantity | Unit |
| Item | |||
| Total mass | 0.1 | kg | |
| Initial angle | 0.05 | ||
| Initial angular velocity | 0.01 | rad/s | |
| Initial radius velocity | 0.1 | m/s | |
| Spring | |||
| Free length | 20 | m | |
| Initial elongation | 2 | m | |
| Elastic coefficient | k | 20 | N/m |
The oscillators equation of motion is as follows
+ a ⋅ (θ (t) – C ) = 0 ( a > 0) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Equation 1
- and are constants.
- constants can be found by rearranging the equation. Such form of equation has the analytical solution like:
θ(t)=A cos (⋅t – ϕ ) +C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Equation 2
- Where
- Angular frequency is
, . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Equation 3
- Amplitude A is given by
. . . . .. .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Equation 4
- And Phase angle is given by
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Equation 5
- when , cos. This is known as the small angle theorem.
discussion
Oscillator has a periodic back and forth motion. Many systems in life can be approximated using oscillator model. Many systems in nature display harmonic oscillation with natural or set frequency which depends on many factors in the system.