Write a program to find the derivatives of sin (x) at point x=1 (given in radians)
Program Part 1
Program Deriv
implicit none
integer ::n,i
real, allocatable :: y(:) dydx(:)
real ::x dx
write(*, ‘(a,$)’) ‘input number of grid points:’ ; read*, n
allocate (y(n), dydx(n)) ! allocate grid arrays
dx = 10.0/(n-1) !grid spacing, assuming x from 0 -10
do i= 1,n
x= (i-1)
y(i) =sin (x) !fill with sine
end do
cal derivative (y, n, dx, dydx) ! calculate dydx
do i= 1, n ! write result, cos(x) and error
x= (i-1) *dx
print*, dydx(i), cos(x), cosx-dydx(i)
end do
deallocate (y, dydx) !finish
contains
sunroutine derivative (a, np, h, aprime) ! argument names different
integer, intent (in) :: np !declare argument
real, intent(in) :: a(np), h
real, intent(out):: aprime (np)
integer :: i local variable
do i=1, np=1
aprime(i)= (a(i+1)- a (i))/h !finite-defference formula
end do
aprime(np) = 0
end subroutine derivative
end program Deriv
Write a FORTRAN program to use Simpson’s rule to evaluate the integral given by
where,, and Indicate in the comment block (at the beginning of your code) what value you obtained for the integral as a function of the number of subintervals used. Make sure to clearly indicate what you think is the most accurate value for the integral.
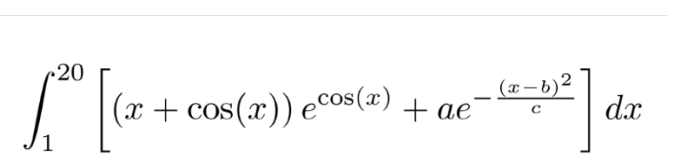
Submit the source code file, i.e. the .f08 file containing the Fortran code, by uploading it into blackboard using the “attachments” button under the assignment. If you have any problems see the TA or the instructor. Submissions via email will not be accepted.
Note:
All programs must contain the implicit none statement. Programs that do not contain this statement will receive an automatic zero.
All programs should have a block of comment statements at the beginning of the code containing your name and a description of what the code does.
All programs must compile using the gfortran compiler on the Math lab machines. Programs that do not compile will receive an automatic zero.
Programs must be uploaded into the blackboard assignment page. Programs may not be submitted via email or hardcopy. Programs that are not uploaded into the blackboard assignment page will not be graded.
Program part 2
Simpsons solition
program integration
! declaring the variable values
real results,simp13_res,simp38_res,a,b,error
real f
integer n
external f
results=0.0
n=0
a=0.0
b=1.0
error=0.0
write(*,*)achar(10),achar(10)
write(*,*)”Intergration of (x^n*e^(x-1)) by dx range of 0 to 1″
10 write(*,*)achar(10)
write(*,*)”Enter 0 to exit from the program”
write(*,*)”Enter n : “
read(*,'(i10)’)n
!to exit
if(n==0)then
goto 20
end if
!factorial function calling
results=factorial(n) !calling the function factorial
write(*,*)achar(10),”Recursion Solution = “,results ! print the value of the function
!get simpson 1/3 solution
call simpson13(f,a,b,simp13_res,real(n))
write(*,*)achar(10),”Simpson 1/3 Solution= “,simp13_res
error=(results-simp13_res)*100/results
write(*,*)”Relative True Error in Simpson 1/3 (%) = “,abs(error)
error=0.0
!get simpson 3/8 solution
call simpson38(f,a,b,simp38_res,real(n))
write(*,*)achar(10),”Simpson 3/8 Solution = “,simp38_res
error=(results-simp38_res)*100/results
write(*,*)”Relative True Error in Simpson 3/8 (%) = “,abs(error)
!continue
goto 10
20 continue
end program integration
! end of the main program, functions are below which is used in this program
!recursive algorithm
recursive function factorial(n) result(results)
real results,first,x
integer n
x=1
first=1/exp(x)
if(n<=0) then
results = 0
return
else if(n==1) then
results=1/exp(x)
return
else
results=1-n*factorial(n-1)
return
end if
end function factorial
!simpson 1/3 algorithm
Subroutine simpson13(f,a,b,simp38_res,n)
real a,b,x,n,h,f,simp38_res
h=(b-a)/2.0
simp38_res=h*(f(a,n)+f(a+h,n)+f(b,n))/3.0
return
end Subroutine simpson13
!simpson 3/8 algorithm
Subroutine simpson38(f,a,b,simp13_res,n)
real a,b,x,n,h,f,simp13_res
h=(b-a)/3.0
simp13_res=h*3.0*(f(a,n)+3.0*f(a+h,n)+3.0*f(a+2*h,n)+f(b,n))/8.0
return
end Subroutine simpson38
!function to integrate
function f(x,n) result(res)
real x,n,res
res=(x**n)*exp(x-1)
return
end function f