Part A:
Here, CC denotes the chocolate chip and OR denotes oatmeal raisin.
Also, per case CC = $70 and per case OR = $65.
Hence, total sales revenue is 70*CC + 65*OR
Therefore, the objective function will be
Max Z = 70*CC + 65*OR
All three machines, Machine A, Machine B and Machine C can be used for production. However, there are few constraints as mentioned below:
For machine A: (1/4)*CC + (1/4)*OR <= 16
Or, CC + OR <= 64 ……… (1)
For machine B: (1/3)*CC + (1/6)*OR <= 16
Or, 2CC + OR <= 96 …….. (2)
For machine C: (1/7)*CC + (2/7)*OR <= 16
Or, CC + 2OR <= 112 ……. (3)
Therefore, in summary the problem will be
Max Z = 70CC + 65OR
Subject to
CC + OR <= 64 ……… (1)
2CC + OR <= 96 …….. (2)
CC + 2OR <= 112 ……. (3)
CC, OR >= 0
Here graphical method has been used to solve this problem:
Step 1: converting inequalities into equations
From (1), we have
CC + OR = 64 …….. (4)
Putting, CC = 0, we have OR = 64; similarly putting OR = 0, we have CC = 64
Hence, equation (4) will intersect y-axis and x-axis at (0, 64) and (64, 0) respectively.
From (2), we have
2CC + OR = 96 …….. (5)
Putting, CC = 0, we have OR = 96; similarly putting OR = 0, we have CC = 48
Hence, equation (5) will intersect y-axis and x-axis at (0, 96) and (48, 0) respectively.
From (3), we have
CC + 2OR = 112 …….. (6)
Putting, CC = 0, we have OR = 56; similarly putting OR = 0, we have CC = 112
Hence, equation (6) will intersect y-axis and x-axis at (0, 56) and (112, 0) respectively.
Now, plotting these equations into graph, we have the feasible region as OXYZAO
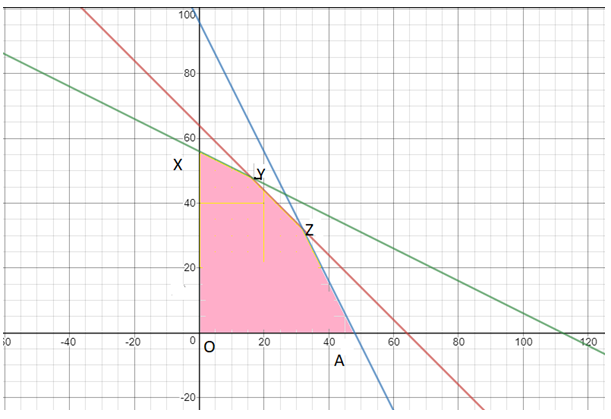
Now, the vertices can be find out considering the intersection theory
Here, X is (0, 56); A is (48, 0), O is (0, 0)
B is intersection point of (4) and (6)
Applying intersection theory, we have y = 48 and x = 16
That is Y is (16, 48)
Similarly, Z is the intersection point of (4) and (5)
Applying intersection theory, we have x = 32 and y = 32
That is, Z is (32, 32)
Now, at O, Z = 0
At X, Z = 0*70 + 56*65 = 3640
At Y, Z = 16*70 + 48*65 = 4240
At Z, Z = 32*70 + 32*65 = 4320
At A = 48*70 + 0*65 = 3360
Hence, Z is the optimal point. In other words, the optimum combination of chocolate chip and oatmeal raisin is 32 cases each.
Part B:
Question 1:
| Chocolate Chip | Oatmeal | |
| Machine A | (1/4)*32*70 = $560 | (1/4)*32*70 = $560 |
| Machine B | (1/3)*32*90 = $960 | (1/6)*32*90 = $480 |
| Machine C | (1/7)*32*120 = $548.57 | (1/7)*32*120 = $1097.14 |
Hence, machine C is cost effective for chocolate chip and machine B for oatmeal.
Question 2:
Maximum number of cases of each kind of cookies:
| Chocolate Chip | Oatmeal | |
| Machine A | 64 | 64 |
| Machine B | 48 | 96 |
| Machine C | 112 | 56 |
Question 3:
| Chocolate Chip | Oatmeal | Labour and Maintenance cost | |
| Machine A | 0 | 0 | $0.00 |
| Machine B | 0 | 32 | $0.00 |
| Machine C | 32 | 0 | $0.00 |
| Total Labour and Maintenance | $0.00 |
| Cost | |
| Machine A | $70.00 |
| Machine B | $90.00 |
| Machine C | $120.00 |
| Set up cost | $300.00 |
| Sales | |
| Chocolate Chip | $70.00 |
| Oatmeal | $65.00 |
| Chocolate Chip | Oatmeal | Hours | |||
| Machine A | 0.25 | 0.25 | 0 | <= | 15 |
| Machine B | 0.333333333 | 0.16667 | 5.333333333 | <= | 15 |
| Machine C | 0.142857143 | 0.28571 | 4.571428571 | <= | 15 |
| Chocolate Chip | 32 | = | 32 |
| Oatmeal | 32 | = | 32 |
| Total Sales | $4,320.00 |
| Production cost | $1,028.57 |
| Total Profit | $2,991.43 |
| Objective Cell (Max) | ||||
| Cell | Name | Original Value | Final Value | |
| $L$10 | Total Profit Sales | -$300.00 | $2,991.43 | |
| Variable Cells | ||||
| Cell | Name | Original Value | Final Value | Integer |
| $D$4 | Machine A Chocolate Chip | 0 | 0 | Integer |
| $E$4 | Machine A Oatmeal | 0 | 0 | Integer |
| $D$5 | Machine B Chocolate Chip | 0 | 0 | Integer |
| $E$5 | Machine B Oatmeal | 0 | 32 | Integer |
| $D$6 | Machine C Chocolate Chip | 0 | 32 | Integer |
| $E$6 | Machine C Oatmeal | 0 | 0 | Integer |
Bibliography
Paris, Q., 2016. An economic interpretation of linear programming. Springer.
Sanchez, L.C. and Herrera, J., 2016. Solution to the multiple products transportation problem: linear programming optimization with Excel Solver. IEEE Latin America Transactions, 14(2), pp.1018-1023.
Uko, L.U., Lutz, R.J. and Weisel, J.A., 2017. An Application of Linear Programming in Performance Evaluation. Academy of Educational Leadership Journal.
Wisniewski, M. and Klein, J.H., 2017. Critical Path Analysis and Linear Programming. Macmillan International Higher Education.