Explaining the thinking about the appropriate arbitrage strategy:

(C) Buy the put option and long the underlying

            The above option is selected to have the appropriate arbitrage strategy, as the put option is considered to be under-priced, where investors should buy it. Therefore, for creating the adequate hedge portfolio the underlying asset also needs to be bought. This measure will mainly allow the created hedge portfolio to generate risk-free rate of return, which is actually higher than the risk-free rate. Thus, the investors for adequately supporting the arbitrage strategy needs to buy the put option and long the underlying.

2. Calculating the continuously compounded risk-free interest rate:

            Therefore, the compounded risk-free rate is calculated at the level of 0.039.

3. Creating an arbitrage opportunity from the European call and put prices of the stock:

	Time 0	Time T
Buy 1 Call at Strike 40	-11	0
Buy 2 Calls at Strike 55	-6	0	0	0
Sell 3 Calls at Strike 50	+18	0	0
Lend $1	-1
Total	0

Premium	11	6	3	0
Strike	40	50	55	50
Amount	1	-3	2	-1
Type	Call	Call	Call	Lend	Payoff
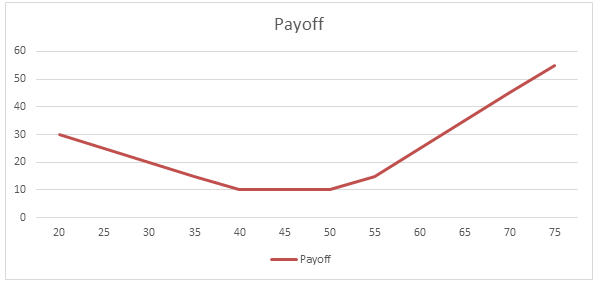
20	-11	48	-6	-1	30
25	-11	43	-6	-1	25
30	-11	38	-6	-1	20
35	-11	33	-6	-1	15
40	-11	28	-6	-1	10
45	-6	23	-6	-1	10
50	-1	18	-6	-1	10
55	4	18	-6	-1	15
60	9	18	-1	-1	25
65	14	18	4	-1	35
70	19	18	9	-1	45
75	24	18	14	-1	55

4.1 Identifying the value of position when share price rises to EUR 1:

            The delta of the position is calculated to be at the levels of zero, where investment is considered to be delta hedged, as no significant change in value is witnessed after increment in share price by EUR 1. The justification of equation is depicted as follows.

Delta Position = Delta – put + number of shares

Delta Position = 0.4330 – 0.5539 + 0.1210

Delta Position = 0.0001

4.2 Indicating how large a change in the stock price is a one standard deviation change over one day:

One day change = Stock price * Standard deviation * √(1/365)

One day change = 40 * 0.30 * √(1/365)

One day change = $0.6281

            The maximum change in the stock price that can be conducted from one standard deviation change over one day is mainly at the levels of $0.6281.

4.3 Stating the position if stock price does not move:

            The no movement of the share price directly have a decay on the two equations, where relevant losses from the position is witnessed by the investor. Thus, the sum of the thetas is mainly considered the loss that will be incurred when there is no price movement of the stock. The loss incurred from the option is represented in the equation, which is depicted as follows.

Loss from no price movement = Theta of Call option + Theta of Put option

Loss from no price movement = -0.0067 – 0.0044

Loss from no price movement = -$0.0111

4.4 Stating the position of stock price move significantly more than one standard deviation:

            The stock price movement in excess of one standard deviation will generate a profit for the investors, as gamma on both positions is positive. Therefore, excess of the standard deviation will result in a profit for the organisation.

5. Stating which of the following portfolio option shows exposure consistent with the report:

D. The trading book has substantial short-expiry long call positions and substantial long expiry short call positions.

Question 6:

Refer to the excel

Question 7:

Refer to the excel

Bibliography:

Walkenbach, J., 2019. Excel VBA Programming. For Dummies.

Zhang, D., Cheng, Q., Agterberg, F. and Chen, Z., 2016. An improved solution of local window parameters setting for local singularity analysis based on Excel VBA batch processing technology. Computers & geosciences, 88, pp.54-66.