# Study sheet 1- Expanding polynomial
- Monomial to trinomial
2x(x2-10x +6x)- Monomial
a (b+ c)= ab + bc
2x3– 20 x2 +6x – trinomial
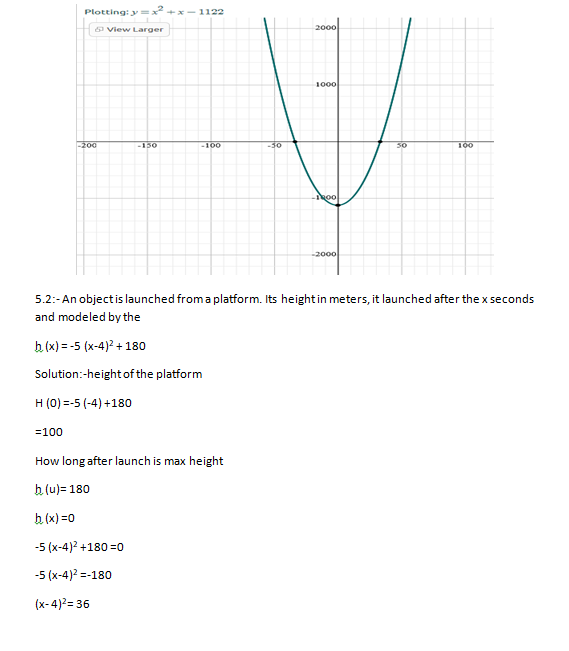
- Binomial into binomial
(4x +2 ) (3x-7)
(ax+b) (cx-d)
On expanding
=acx2 –axd +bcx – bd
=acx2 – (ad-bc)x – bd
4x (3x-7) +2 (3x-7)
=12x2 -22x -14
- Vertex form to standard form
Vertex: y= a(x-b)2 +k
Standard form: y= ax2+ bx +c
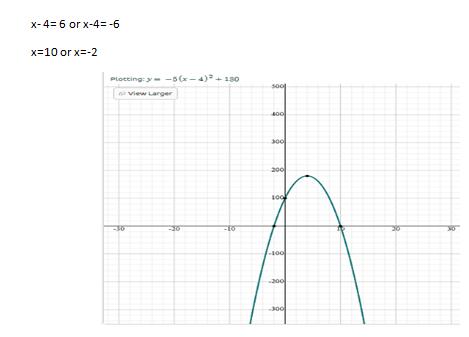
Y= 2[(x+1)2] -5: Vertex form
Y= 2[(x+1) (x+1)]-5
Y= 2(x2+2x+1) -5
Y= 2x2+4x+2-5
Y= 2x2 +4x-3
Standard form
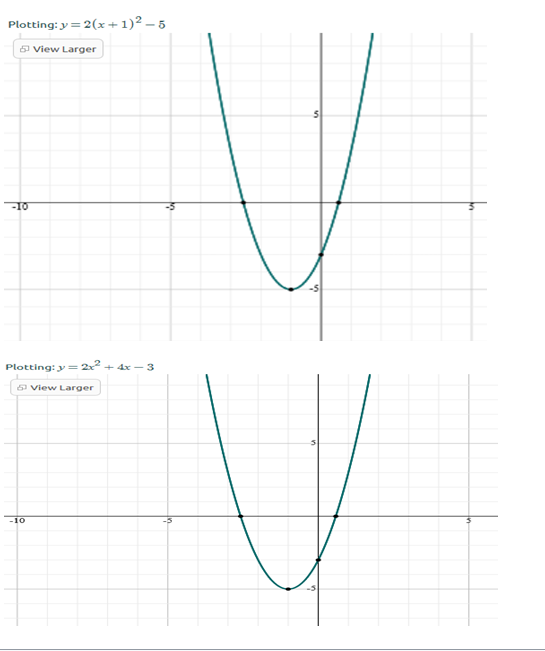
4. Factored form to standard form
Y= 3 (x+3) (x+2): Factored form
Y= 3 (x2 + 2x + 3x + 6)
Y= 3 (x2 + 5x + 6)
Y= 3x2 + 15x + 18 standard form
# Study Sheet 2: Factoring
1. Method of Common
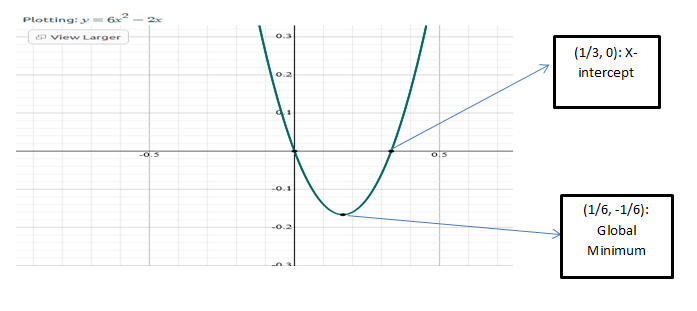
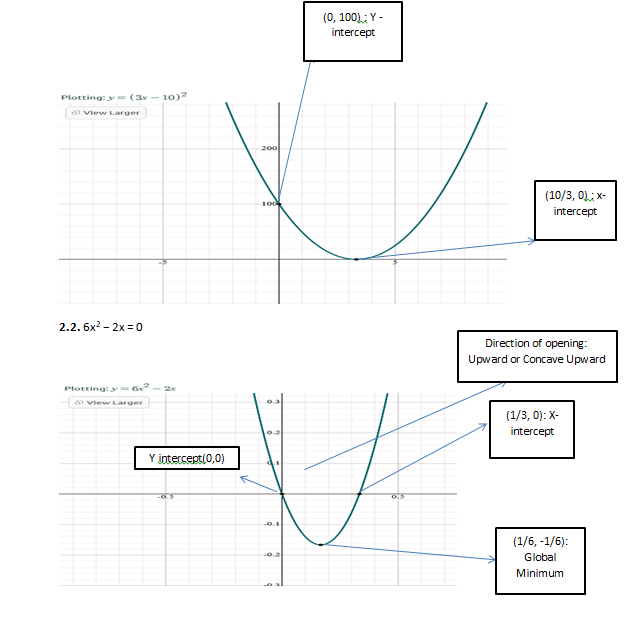
6x2 − 2x = 0
2x 3 x X x X – 2x =0
2x ( 3x -1) =0
Common: 2x
2. Y = grouping
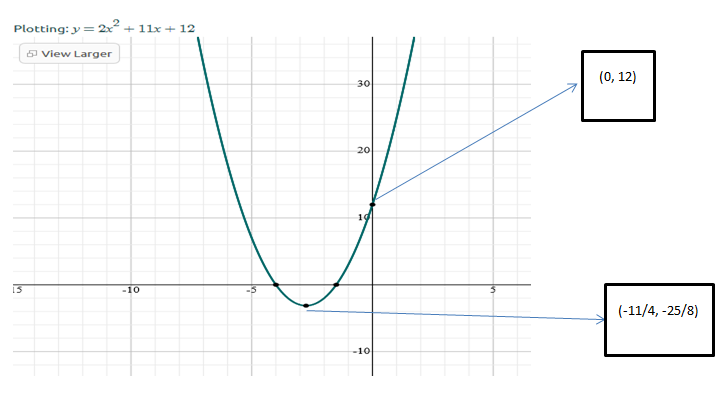
2x2+8x+3x+12
Ist grouping (2x2+8x)
Second grouping (3x+12)
=2x(x+4) +3 (x+4)
=(x+4)(2x +3)
= 2x^2+11x+12
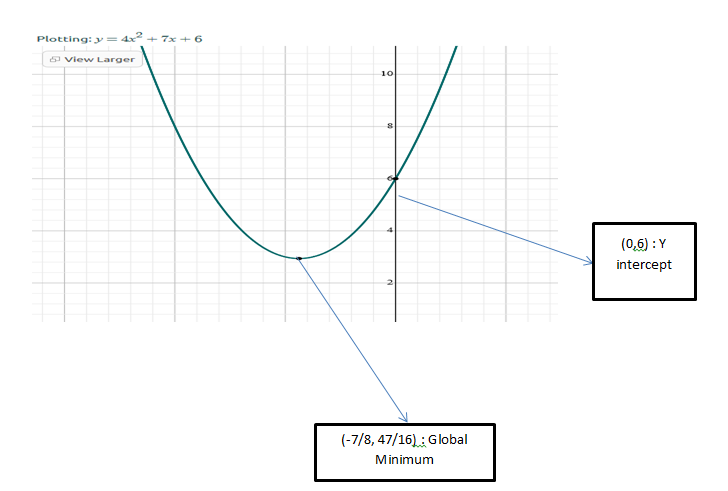
3. x2 + 7x + 6
= x2 + x + 6x + 6
= x(x + 1) + 6(x + 1)
= (x + 1)(x + 6)
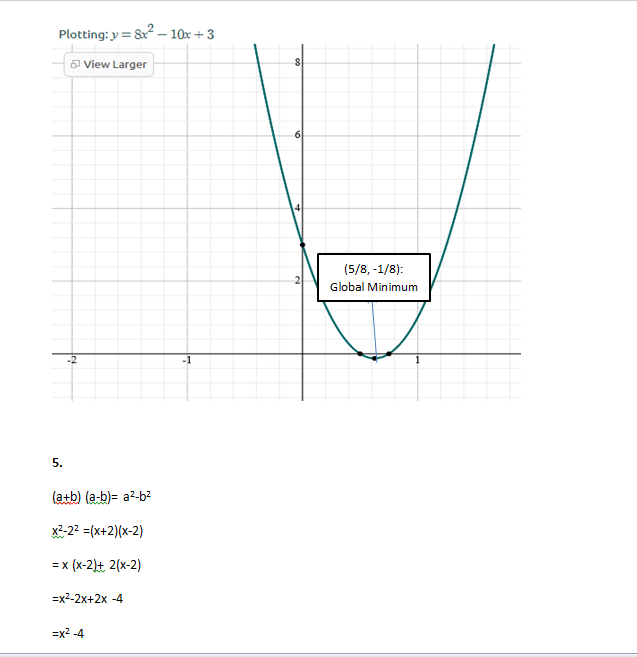
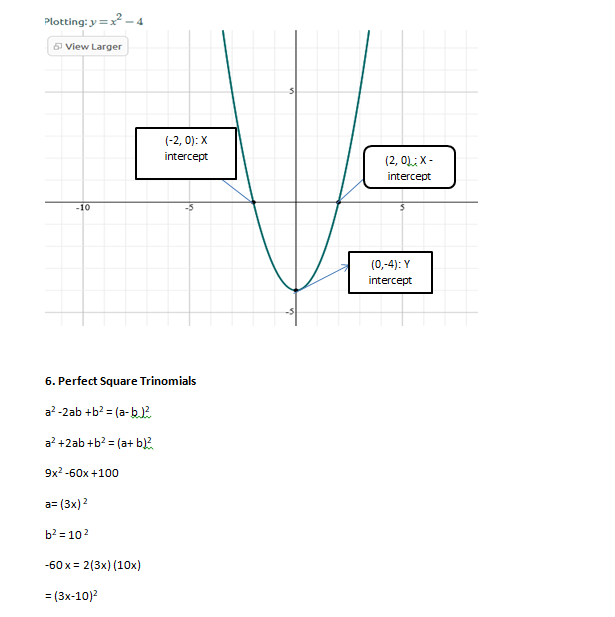
4:- Trinomial Shortcut
8x2– 10x +3
8x2– 10x +3
x2-10x +24
(x-4) (x-6)
x=4, x=6
# Study Sheet 3: Finding the Vertex
- F(x) = ax2 +bx +c opens upward: Concave Up
F(x) = -ax2 +bx +c opens downward: Concave Down
Y= 2x2 -8x +5
X=- b/2a
F (b/2a)
(-b/2a, f (-b/2a))
X=-b/2a
X= -(8)/2(-2)
X=8/4
=2
Y= 2x2 -8x +5
a=2, b=-8, c=5
F(2) = 2(2)2 -8 x 2 +5
Y=-3
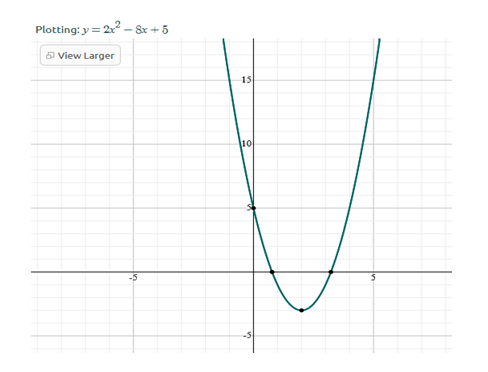
(2, -3)
- F(x) = ax2 +bx +c
Vertex form to completing the square form
Vertex form: y= a(x-h) 2 +k
Step 1:- y = ax2 +bx +c
Y= 2x2 – 4x +5
So move + 5 to the other side
y- 5 =2x2– 4x
Step 2:- Factor out can current leading coefficient
y- 5 = 2 (x2 – 2x)
Step 3:- Create a perfect square Trinomial
y- 5 + 2
=2 (x2 -2x+ )
Step 4:- Take half of the coefficient of x term inside the paarthesis square and put its value into box
y- 5 + 2
Step 5:- Simplify y-3 =2 (x-1) 2
Step 6:- Isolate y term y= 2(x-1)2 + 3
Step 7:- Vertex form of equation
y= a (x-h)2 +k
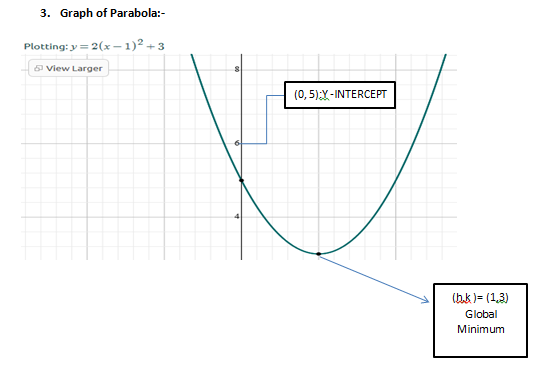
v (1,3)