1- With first order decay rate constant kA and kB. A liquid waste stream contains dissolved A at concentration CA,o (mol m-3) and no B or C. This waste stream has a flow rate of Q and enter a complete mixed reactor of volume V.

• What is the expression for steady state exit concentration for A?

• What is the expression for the steady state exit concentration of B?

• What is the expression for the steady state exit concentration for C?

2. You are asked to design a reactor to increase the level of oxygen in groundwater (to be used as drinking water) from 2 mg/L to 7 mg/L O₂. Two different types of reactors are to be considered (1) a CFSTR, or (2) a sequencing batch reactor (SBR), in which the reactor is filled, left to react, emptied, and the cycle is repeated. It takes 5 min each to fill and empty the reactor (10 min total of filling and emptying time per cycle). In either configuration, air is bubbled through by diffusers in the bottom. Determine which reactor can achieve the treatment goal in less time, given the following information:

d

Solution

Lowest size of the reactor needed

If a CFSTR is used instead of SBR, volume of reactor needed will be calculated as

The required size for CFSTR is 133.286 L.

Thus CFSTR will be the most appropriate one.

3. In this problem you will design an adsorption system to remove compound A from water with granular activated carbon (GAC). The system consists of two batch reactors that contain the same dose of GAC, and treat water sequentially (i.e., first a batch of water is treated in reactor 1 and then in reactor 2).

• First you need to develop an equation for the adsorption isotherm of compound A onto activated carbon. After conducting experiments in the laboratory, you have the following data. Assume the adsorption can be described by a Freundlich isotherm ( ) and determine the values of  and .

CA	Q
mol/L	mol/g
1.9	6.2
21.0	22.5
42.3	33.0

Applying logarithm on both sides (Elio Santacesaria, 2018)

We create a new table

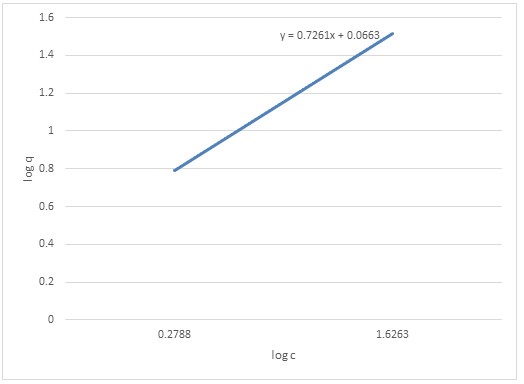
Log C	Log q
0.2788	0.7924
1.3222	1.3522
1.6263	1.5185

We graph our new data

We use the line of best fit to generate the straight curve as show with dotted lines.

From the linear equation;

• Calculate the dose of fresh GAC needed to reduce the concentration of compound A from 50 mol/L to 20 mol/L in the first reactor.

• In the second reactor, you treat the water from the first reactor with the same GAC dose. Use a graphical approach to determine the final concentration of compound A. (i.e., draw a graph of q vs. C_A showing the Freundlich isotherm, then draw the system path for the 2 reactor

• 

The isotherm curve is represented by the dotted lines and the solid line represents the system path.

4. A stripping column is designed to remove chloroform (a chlorine disinfection by-product) from treated drinking water. The treatment goal is to reduce chloroform from 120 to 30 μg/L.

• Calculate the effluent concentration of chloroform ( ) given the following:

• Draw a graph of  vs.  (both in μg/L) showing the line for Henry’s Law and the operating line for the stripping column

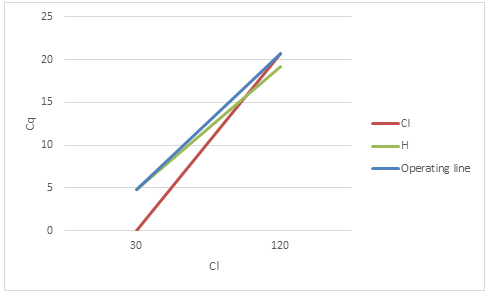
• What is the rate of gas transfer at the top of the stripping column? (in μg/L-s)

5. A batch reactor is used to conduct kinetic studies to define the rate constant for the following reaction. It is hypothesized that the reaction rate expression is of the form r_A = -kC_A^α (it is already known that the rate is zero-order with respect to B).  The data shown in the table are collected.

Time, min	CA, mol/L
0	10
1	4.0
2	1.65

• Determine the value (and units) of the rate constant k.

Differentiating the expression we obtain

Rearranging and integrating (Schmal, 2014);

                             …………….. (i)

When ,  and substituting in (i),

Hence, equation (i) becomes

 ………………..(ii)

When , . Substituting in (ii)

 ……………(iii)

When . Using this values in (iii)

…………………..(iv)

Dividing (iii) by (iv);

Solving for

Substituting back in (iv) and solving for

• If the initial concentration of A is 75 mol/L and the initial concentration of B is 60 mol/L, how much B is left after 30 s? (in a batch reactor)

When

6. A subsurface site has spilled a nonaqueous phase liquid that is composed of only two compounds, each at a mole fraction of 0.5. These compounds have the following properties:

Compound	MW	Vapor Pressure	Water Solubility	Octanol Water Partition Coeff.
	g/mol	Pº, kPa	Cw,sol, g/m3	Kow
Hexane	86	20.2	9.5	1.3 x 104
Nonane	128	0.57	0.12	x 106

• What initial contaminant concentrations in water would you predict if the groundwater used to recover the contaminants?

For hexane;

For nonane;

• What initial mass concentrations in gas would you predict if air was used to volatilize the contaminants?

For hexane;

For nonane;

7. An experiment to determine compound partitioning among air, water, and solid phases was conducted by adding 1 gram of the compound to a reactor that had 1 m³ of air, 10^-3 m³ of water, and 100 g of solid. The reactor was at atmospheric pressure, and at a constant temperature of 20ºC (293K). The compound has a molecular weight of 110 g mole^-1. Once equilibrium is reached, the air has a mass concentration of 0.400 g m^-3, and the water has a mass concentration of 250 g m^-3.

1. Determine the value of the Henry law constant for the compound, H_cA.

Henry’s law constant

Where P is the partial pressure and  is the mole concentration of the compound (Fogler, 2013).

From ideal gas equation

Moles of the compound

Thus,

• Given that adsorption between water and the solid phase for this compound is linear, determine the isotherm constant.

Where m is the mass of solid, c concentration of the compound and X is the mass of adsorbent.

Thus,

• If the solid phase were completely removed from the air and water, and then resuspended in 10^-3 m³ of initially clean water, what would be the contaminant concentration in the water once equilibrium is attained?

References

Elio Santacesaria, R. T., 2018. The Chemical Reactor from Laboratory to Industrial Plant. In: A Modern Approach to Chemical Reaction Engineering with Different Case Histories and Exercises. s.l.:Springer, pp. 111-198.

Fogler, H. S., 2013. Elements of Chemical Reaction Engineering. In: Always Learning. s.l.:Pearson Higher Education & Professional Group, pp. 236-435.

Schmal, M., 2014. Chemical Reaction Engineering. In: Essentials, Exercises and Examples. s.l.:CRC Press, pp. 123-176.