Checking assumptions
- Linearity can be assumed
- The data is linear
- Normality of errors can be assumed
- The histogram of errors can be assumed
- Homoscedasticity can be assumed
- The variation about the regression line is constant for all values of the independent variable
- Independence of errors can be assumed
- The residuals are independent for each value of the independent variable
- Therefore, the assumptions are met.
Scatter plot
The scatter plot below shows that there is a positive linear relationship between Yards per game and Points per game. An increase in the Yards per game is expected to result in an increase in the Points per game.
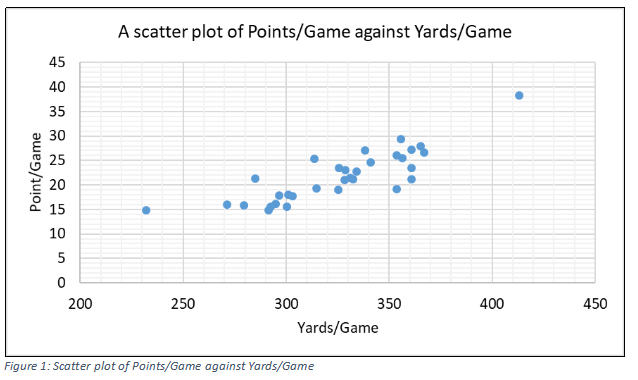
Figure 1: Scatter plot of Points/Game against Yards/Game
Outliers
From the above graph, we can see that there are two outliers
Regression analysis
A regression analysis was performed to try and predict the Points per game based on the Yards per game. Results are presented below;
The summary output table shows that the value of R-square is 0.711; this implies that 71.1% of the variation in the Points per game is explained by the Yards per game.
| Table 1: SUMMARY OUTPUT | |
| Regression Statistics | |
| Multiple R | 0.843181 |
| R Square | 0.710955 |
| Adjusted R Square | 0.70132 |
| Standard Error | 2.869583 |
| Observations | 32 |
| Table 2: ANOVA | |||||
| df | SS | MS | F | Significance F | |
| Regression | 1 | 607.6236 | 607.6236 | 73.78994 | 1.39E-09 |
| Residual | 30 | 247.0351 | 8.234505 | ||
| Total | 31 | 854.6588 |
The ANOVA table above shows the p-value for the F-Statistics to be 0.000 (a value less than 5% level of significance), we therefore reject the null hypothesis and conclude that the overall regression model is significant at 5% level of significance.
Table 3: Regression coefficients
| Coefficients | Standard Error | t Stat | P-value | Lower 95% | Upper 95% | |
| Intercept | -18.2288 | 4.682343 | -3.8931 | 0.000512 | -27.7915 | -8.66621 |
| Yards/Game | 0.122941 | 0.014312 | 8.590107 | 1.39E-09 | 0.093712 | 0.15217 |
Lastly, the above table (table 3) presents the regression coefficients. As can be seen both the intercept and the independent variable (Yards/Game) are significant in the model at 5% level of significance (p < 0.05).
The coefficient of Yards/Game is 0.1229; this implies that a unit increase in the Yards/Game is expected to result in an increase in the Points/Game by 0.1229. Similarly, a unit decrease in the Yards/Game is expected to result in a decrease in the Points/Game by 0.1229.